Puzzle Board
In mathematics, shapes that have self-similarity are called fractals. They have an infinite pattern that appears similar no matter how closely you look at them. Students can explore the Fractal Course on Mathigon as an introduction to fractals. Having the same pattern in every scale of the main shape is just a small part of the fascinating properties of fractals.
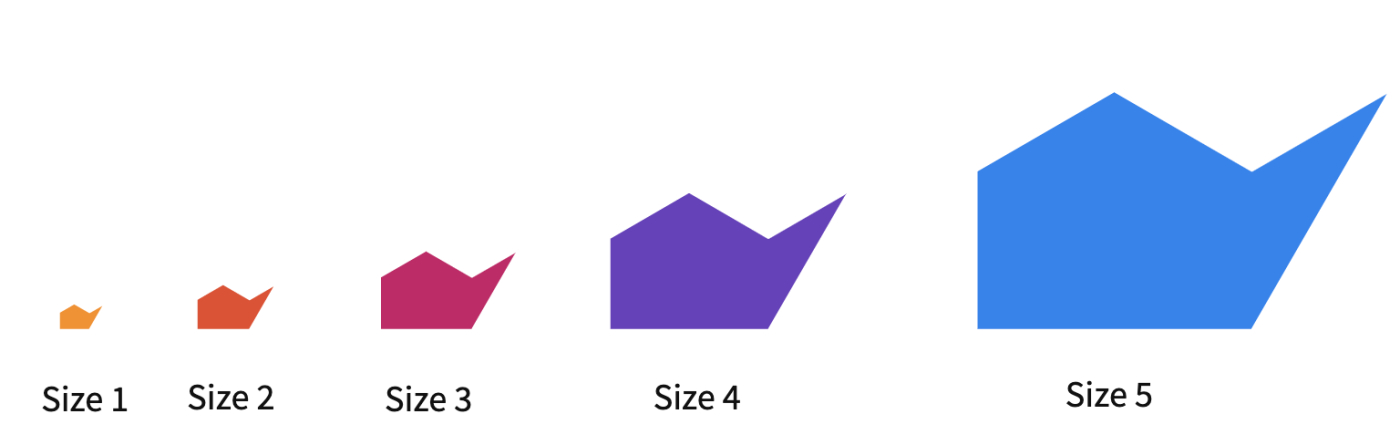
There are ready-to-use fractal tiles on Polypad. These are concave hexagons in five different sizes.
Hints
There are several ways of making the following sizes. You can discuss some possible strategies to create the next shape. For example, you may ask students to analyze the shapes. They can start with creating the existing shapes to realize they can be formed using regular hexagons, equilateral triangles, and even the Penrose tiles; kite and dart.
Another easy and surprising method would be using the existing fractal designs.
Solution
More on the Complete the Fractal Puzzle
Please visit the Fractals Unit on the Polypad tasks page to explore the fractal tile designs more as well as the many other interesting types of fractals you can create with Polypad!
Next
If you like this puzzle, try this one!