整除和素数素数的分布
检测素数的最简单方法是,尝试用所有比它小的数去整除它。计算机能非常快速而有效的做这个 工作。即使对于有着数百位的__非常__大的数,也存在许多高效的算法。甚至其中一些 算法是利用概率来__近乎确定__的测定一个数是否为素数。
这是一个可以让你检查任何数字是否是素数计算器:
素数检测程序
${result}
纵观历史, 人们试图不断的找到越来越大的素数。在1460年,已知的最大素数是13,1071。 在1772年,
随着20世纪计算机的到来,计算大素数变得容易多了。目前我们知道的最大素数是在 2018年12月发现的,而且它有24,862,048位数。你需要8000张纸才能把它完整打印出来!

GIMPS(伟大的互联网梅森素数研究)是一个协作项目,志愿者可以使用 免费软件寻找数素。
计算求解这些大素数也许看来像在浪费时间,但是在这堂课程后面你将了解到各种实际 应用程序,其中的计算机必须使用大素数。
这里可以按照指定的位数生成你自己的大素数:
素数生成器
位数:
${result}
乌拉姆螺旋
波兰数学家
我们把所有数字写在一个矩形格子中,从中间以1开始,然后向外螺旋展开。然后我们 加亮突出显示所有的素数。
到目前为止,乌拉姆螺旋线看起来并不特别令人兴奋。但如果我们缩小,有趣的模式就 会出现。这是高达160,000时素数的分布样子:
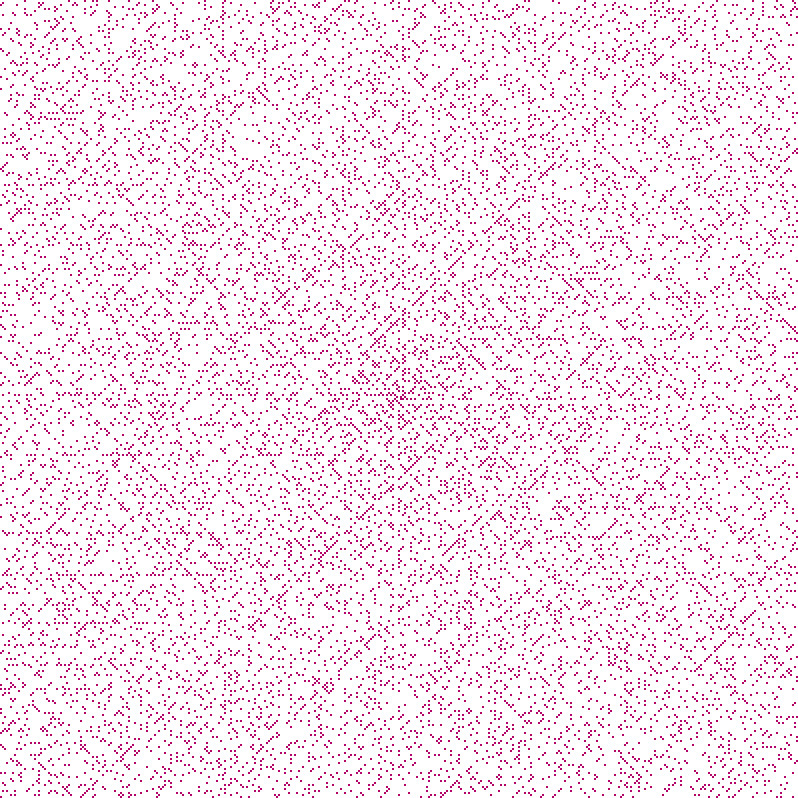
正如人们所期望的那样,某些对角线似乎比其他对角线更受素数欢迎,而不是随机出现。 这创造了一个奇怪的“格子”图案。
结果表明,这些对角线都对应于某些二次方程,这些方程似乎比平均数生成 素数的频率更高。然而,尚不清楚为什么会是这样...
1964年3月版《科学美国人》的封面
哥德巴赫猜想
在1742年, 德国数学家
哥德巴赫计算器
任选一个偶数,算算它
如何被写成两个素数的和.
${result}
哥德巴赫在给著名数学家
计算机已经检查了哥德巴赫猜想对每一个最大可达4×1018(这是一个4后面18个 零)的偶数都有效,但数学家们仍然没有找到它对_所有_偶数都有效的证明。这是一个很大 的区别,因为有无限多的整数,所以我们不可能检查所有的整数。
其明显的简单性使哥德巴赫猜想成为数学中最著名的未解决问题之一。
孪生素数
我们已经清楚素数随着整数变大而分散得越来越开。但它们总是看起来像完全随机的,偶 尔我们还会发现两个素数紧挨着,就像一个整体:它们被称为__孪生素数__。
35,1113,4143,101103,20272029,108,377108,379,1,523,6511,523,653
已知最大的一对孪生素数有惊人的58711位!但是有无限多的孪生素数吗,就像有无限多的 素数一样?没有人知道答案 -- __孪生素数猜想__是围绕着素数的许多未解决问题中的另一个。
黎曼猜想
数学家们花费了许多个世纪来探索素数的模式和分布。它们看起来完全是随机的——有时连 续的素数之间有巨大的间隙,而有时我们又会发现紧挨着的
当德国数学家
沿x轴可以看到所有整数。当有素数时,_{.m-blue}素数计数_增加1。当我们
高斯注意到这个函数的形状看起来和函数
然而,正如您在上面看到的,在实际素数和高斯近似值之间仍然有一个很大的误差。 1859年,数学家
数以百计的数学家试图证明黎曼猜想,但都没有成功。它通常被认为是数学中最困难和 最重要的未解决问题之一。2000年,克莱数学研究所称它为六个