分形引言
环顾大自然时,您可能已经注意到像这样的复杂植物:


这种__蕨类植物__ 由许多小叶子组成,而这些小叶子又是从较大的叶子分支出来


这种 罗马花椰菜 由较小的
一眼看去,它们像是非常复杂的形状 -- 但是当你仔细观察时,您可能会注意到它们都遵循一个相对简单的模式:这些植物的所有单独部分看起来与整个植物完全一样,只是更小,同样的模式在更小的尺度上不断重复。
在数学中,我们将这种特性称为 自相似性,并将具有此特性的形状称为
要创造我们自己的分形,必须从一个简单的图案开始,然后在较小的尺度上不断重复它。
最简单的模式之一可能就是一条线段,其中还有另外两条线段从线段的一端分叉出去,如果我们重复这种模式,两条蓝色线段的末端还将有两条线段分叉出去。
您可以通过移动蓝色点来改变所有分支的长度和角度,然后使用下方的
根据分支的位置,您可以创建出完全不同的模式 -- 看起来像上面的、一棵 或 。你还能创建出什么呢?
另一个著名的分形是
请注意,最终形状是如何由自身的三个相同副本组成的,而每个副本又是由整个三角形的更小副本组成!您可以一直放大这个三角形,这些模式和形状会一直重复。
本章开头的植物 看起来 就像分形,但在现实生活中显然不可能创建出 真正的 分形。如果我们不断重复同样的模式,并且越来越小,最终我们会得到无法再分裂的细胞、分子或原子。
但是,利用数学,我们可以思考真正的分形“将”具有的性质 - 这些是非常令人惊讶的……
分形维数
首先,让我们看一下分形的维数,一条线的维度是
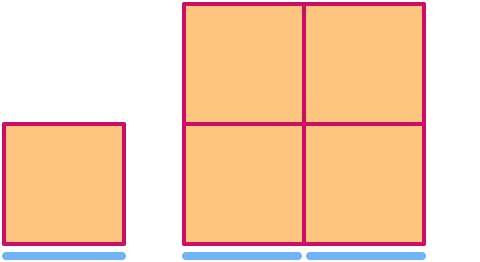
正方形的维度是
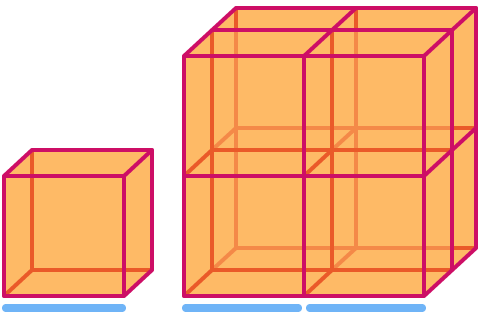
立方体的维度为
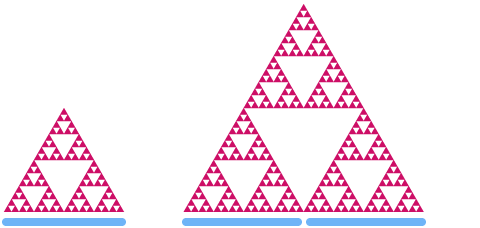
现在让我们看一下谢尔宾斯基(Sierpinski)三角形,如果我们将尺寸放大2倍,可以看到它的“面积”增加了
假设 d 是谢尔宾斯基(Sierpinski)三角形的尺寸,应用与上述同样的模式,我们得到
但是,等等……一个东西的维度怎么可能不是整数呢?这似乎是不可能的,但这只是分形的奇特属性之一,事实上,这就是分形得此名的原因:它们具有__分数维__。
每次迭代时,我们都会占用掉谢尔宾斯基(Sierpinski)三角形的部分区域,如果我们可以无限次这样做,那么实际上就没有剩余的面积了:这就是为什么谢尔宾斯基(Sierpinski)三角形是介于于二维面积和一维线之间的原因。
虽然许多分形是 自相似的 ,但一个更好的定义是,__分形__是具有__非整数维__的形状。
科赫雪花
自然界中有许多看起来像分形的形状。在本章开始时,我们已经看到了一些植物例子,另外一个很好的例子是雪花和冰晶:
要自己创建分形雪花,我们必须再次找到一个可以反复应用的简单程序。
与谢尔宾斯基(Sierpinski)三角形一样,让我们从一个单一的等边三角形开始,但是,我们没有 在每个步骤中去移除 更小的三角形,而是沿边缘 添加 更小的三角形,每个三角形的边长是上一步骤中三角形的
产生的形状称为
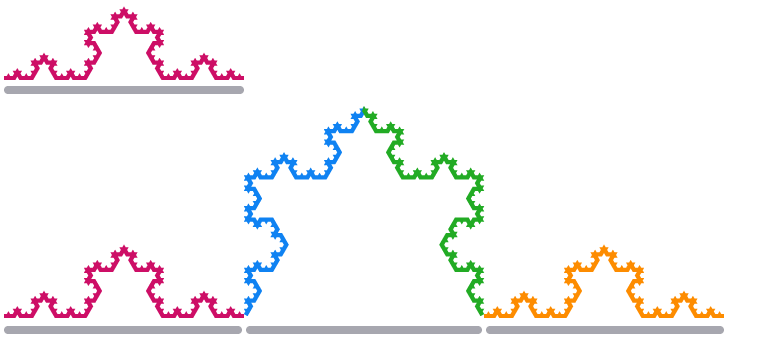
当我们将科赫雪花(Koch Snowflake)的一个边缘部分放大3倍时,其长度变为
使用与上面提到的维度与缩放比例之间的关系,可以得到公式
面积_{span.check(when="blank-6")}_
创建科赫雪花(Koch Snowflake)就像创建一个




第一次迭代后,每一步新的三角形数量增加了
假设
使用无穷
周长_{span.check(when="blank-9")}_
我们还可以尝试计算科赫雪花(Koch Snowflake)的周长。正如我们之前已经看到的,周长在每一步都会改变
这意味着我们有一个等比数列 - 但是在本例中,它

如果这似乎违反直觉,请记住,我们在每一步都将周长乘以
现在你拥有一个_有限_面积和一个_无限_周长的形状,这简直不可思议 – 但这只是分形的许多意想不到的特性之一。
您能否想出其他方法来创建自己的分形吗?
“我的灵魂在周围冰冻的分形上旋转……”
门格海绵
分形不一定要像上面的许多示例一样是“扁平的”。最著名的三维分形之一是__门格海绵(Menger sponge)__,以数学家
我们从一个实心的立方体开始,不断地在它的侧面钻出越来越小的孔,每一次新迭代孔的宽度都是上一次迭代孔的宽度的
一个
现在,我们可以像上面的科赫雪花一样,尝试计算一下门格海绵(Menger sponge)的尺寸_d_,在这种情况下,我们得到
想像一下,如果您无限次地切出越来越多的孔,那么实际的体积就没有了,这就是为什么立方体是“不完全的”三维!
分形海岸线
到目前为止,我们所看到的所有分形的关键特征是,你可以一直“放大”,并始终能找到符合同样模式的新的图案。 1920年左右,英国数学家
首先来看一个国家的基本形状,随着你不断放大,可以看到河流入口、海湾,然后是悬崖、岩石,等等:
在计算一个国家的边境线长度时,一个重要的问题是 – 你如何决定放大多大,要包括哪些角落和裂缝?
例如,测量英国海岸线的长度,我们可以有一种方法,拿起一把长尺,绕着海滩走一圈,然后将所有的距离加起来。
如果标尺长
我们可以继续,用越来越小的尺子,每次我们得出的海岸线长度都会更长一些。就像前面的科赫雪花一样,英国的海岸线似乎是无限长!这通常被称为__海岸线悖论__。
几十年后,数学家
英国的海岸线确实“看起来”是分形的,但它却不像我们之前看到的其他分形那样是 自相似 的,为了找到它的大小,我们可以将其绘制在网格上,并计算它与多少个单元格相交。
最初有__{.pill.yellow} 88__个相交单元格,如果我们将海岸线缩小1倍,则有__{.pill.yellow} 197__个相交的单元格 – 是之前的两倍多!
海岸线的长度增加了
如果在更大的网格上重复这个过程,我们会发现英国海岸线的维数实际上约为 1.21。曼德勃罗(Mandelbrot)意识到,这种分形维数也是形状__粗糙度__的一种度量,这是一个全新的概念,并且他在数学和科学的许多其他领域发现了重要的应用。
自然与科技中的更多分形
尽管真正的分形永远不会出现在自然界中,但有很多物体看起来 几乎 就是分形。我们已经看过植物、雪花和海岸线,这里还有更多的例子:
位于中亚的山脉
印度的恒河三角洲
闪电
视网膜上的血管
美国大峡谷
云朵
所有这些物体的形状看起来可能都是完全随机的,但就像分形一样,存在一个潜在的模式决定了它们是如何形成的,数学可以帮助我们更好地理解这些形状,分形在医学、生物学、地质学和气象学等领域都有应用。
由计算机生成的分形地形
我们也可以使用分形来创建逼真的自然“复制品”,例如,用于视频游戏或计算机生成的电影中的景观和纹理,左图中的水,山和云完全是由计算机利用分形完成的!
我们甚至可以逆转此过程来压缩数字图像,以减小它们的文件大小。最早的算法是由迈克尔·巴恩斯利(Michael Barnsley)和艾伦·斯隆(Alan Sloan)在20世纪80年代开发的,而新的算法至今仍在研究之中。