分形曼德布罗特集

我们在前面章节中看到的所有分形都是通过__迭代__的过程创建的：首先从一个特定的模式开始，然后不断地重复。

这和你之前看到的另一个数学概念很相似：用递归序列，从一个特定的数字开始，然后不断重复应用同样的递归公式，以得到序列中的下一个数字。

让我们以递归公式 xn=xn−12 为例，将其项绘制在数轴上。您可以更改x0 的值：

请注意，根据起始值 x0 的不同，得到的结果序列所表现出的行为会有很大不同：

到目前为止，我们还没有学到任何新的东西。但是，大约在一个世纪以前，数学家们开始探索如果使用复数而不是仅仅使用实数数轴，这些序列会发生什么。他们的发现是整个数学当中最令人惊讶和最美丽的结果之一。

朱莉娅集

让我们使用与之前相同的序列 xn=xn−12，但要在复平面上进行。您可以移动x0的位置，查看。如果序列看起来会收敛，就用 蓝色 为平面上的相应点着色：

可以看到，只要x0位于单位圆单位正方形外部 _x_轴上方 （以原点为中心，半径为1的圆）内，该序列就收敛。

下面来点稍微难的，不仅仅是取前一个数字的平方数，每次还添加了一个常量 c （可以是任何复数），换句话说，xn=xn−12+c，你认为还会得到收敛圆吗？你认为我们会看到什么样的形状？ 继续

在此图中，您可以移动x0的位置，调整c 的值：

通过数字着色形成的不同形状称为Julia集。它是由两位法国数学家加斯顿.朱利亚（Gaston Julia）和皮埃尔.法图（Pierre Fatou）于1918年各自独立发现的。

在那个时候，没有计算机可以帮助我们直观地看到Julia集的实际样子，像朱利亚（Julia）和法图（Fatou）这样的数学家能够从数学上对它们进行推理，但他们只能看到粗略的手绘草图。

这个问题在今天就不存在了，下面的图片是所有不同的Julia集，不同的颜色表示序列在该点的发散有_多快_：

继续

曼德布罗特集

当创建不同的Julia集时，你可能已经注意到，_c_的某些值对应的每个序列都发散了，整个复平面留下是白色的。在朱利亚（Julia）和法图（Fatou）之后的几十年，新一代的数学家试图绘制出这些区域的样子。

在前面的示例中，我们为 c 选择了一个固定值，然后改变x0的位置以对平面着色。现在，我们让我们先设定固定值 x0=0，而不是改变 c的值。

再一次，在复平面上绘制以显示序列仍处于边界的区域，你希望看到什么形状？

xn=xn−12+${complex(c)}

x0=${complex(x0)}

x1=${complex(x1)}

x2=${complex(x2)}

x3=${complex(x3)}

…有界!发散!

这种分形称为曼德布罗特集（Mandelbrot Set），当旋转90°时，它看起来像一个有头有身有两条手臂的人，数学家 Robert Brooks 和 Peter Matelski 在1978年的一份研究论文中首次定义和绘制了它：

几年后，Benoit Mandelbrot 使用了IBM强大的计算机为分形创建了更为细致的可视化效果，这些分形后来以他的名字命名。第一批打印输出的分形看起来与他预想的不一样，直到他意识到打印机技术人员正在清理其边缘的“模糊”部分（他们认为它是由灰尘颗粒或打印机错误引起的，而不是由于对分形特征的定义造成的） ！ 继续

像所有分形一样，我们可以一直不断“放大” 曼德布罗特集（Mandelbrot Set），在各个尺度下都可以找到一种新的模式。在这里你可以放大曼德布罗特集（Mandelbrot Set）中称为__海马谷__的这部分，黑色点位于 曼德布罗特集（Mandelbrot Set） 内 ，这里的序列是收敛的，其它有颜色的点位于 曼德布罗特集（Mandelbrot Set）之外，这里的序列是发散的，不同的颜色表示它 增长到无穷大的速度 有多快：

Scale: ${pow(scale)}

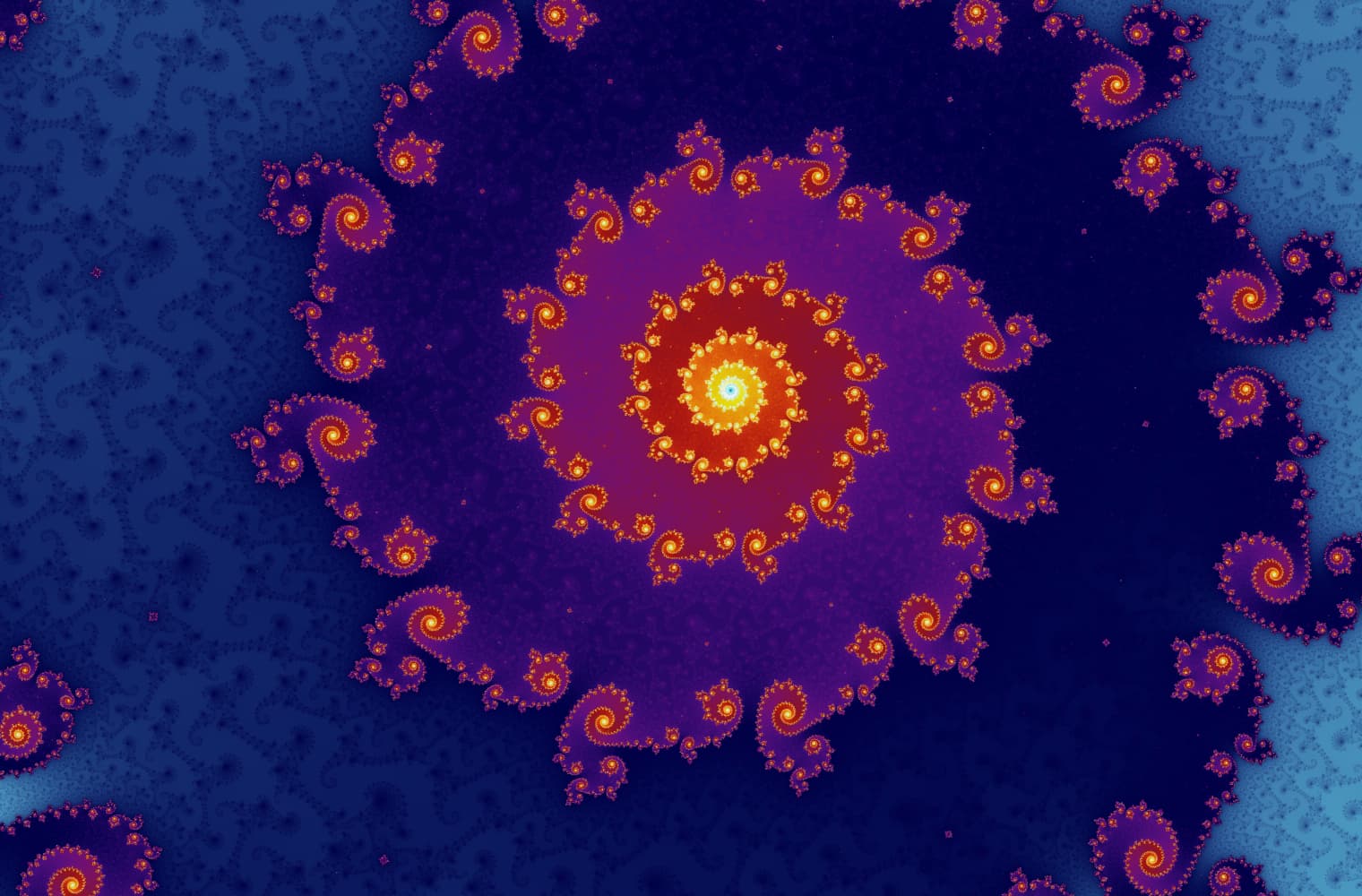
该滑动条由 27 幅单独的图像组成，最大可以达到14兆或254倍的缩放级别，在一款现代笔记本电脑上进行渲染，总共花了将近45分钟。曼德布罗特集（Mandelbrot Set）可以用一个简单的方程 xn=xn−12+c 来来创建，但它却又是无限复杂的，而且非常漂亮。

当你在曼德布罗特集（Mandelbrot Set）周围移动 c的值时，您可能会注意到一个奇妙的性质：

• 曼德布罗特集（Mandelbrot Set）的主体部分内的所有序列都是 收敛发散沿一个轨迹 到一个点。
• 在顶部球状体内的所有序列 形成一条轨迹收敛发散 它由个点组成。
• 在较小球状体里的序列有一长度为 的轨迹。

每个球状体都有不同大小的轨道，越小的球状体在其轨道上的点越多。这些轨道的大小与混沌理论中的重要概念__单峰映象（logistic map）__密切相关。