序列和模式算术序列和几何序列

在1682年，天文学家埃德蒙·哈雷发现了一个不寻常的现象：一个发光的, 有一条长长尾巴的白色物体，在夜空中移动。它是一颗__彗星__，一块在太空中飞行时留着一道冰尘尾巴的小冰石。

哈雷记得其他天文学家早就观察到类似的彗星：一次在1530年，另一次在1606年。注意，这些观察结果之间的差距是相同的: 年。

哈雷彗星图片，
1986年拍摄于复活节岛

哈雷得出结论: 这三次观测结果实际上都是同一颗彗星 — 现在被称为__哈雷彗星__。它围绕太阳运行，大约每76年经过一次地球。他还预测了彗星下一次出现的时间：

1530, 1606*{span.arrow}+76*, 1682*{span.arrow}+76*, 1758*{span.arrow}+76*, +76, +76, +76, …

事实上，该时间间隔不总是__精准__的76年: 它可能有1或2年的变化，因为彗星的运行轨道受到其它行星的干扰。今天我们知道哈雷彗星早在公元前240年就被古代天文学家观测到了！

哈雷彗星在时间上的分布：巴比伦的石碑（公元前164年）、中世纪的挂毯（1070年代）、科学杂志（1910年）和苏联的邮票（1986年）。

另一组科学家正在调查一个有弹性的网球的行为。他们把球从10米的高度扔下，并测量了它随时间变化的位置。每次弹跳，球都会损失原来的一部分高度：

科学家们注意到，每次弹跳后，球会失去其高度的20%。换句话说，每次弹跳的最大高度是前一次弹跳的80%。这使他们能够预测以下每一次弹跳的高度:

10, 8*{span.arrow}×0.8*, ×0.8, ×0.8, 4.096*{span.arrow}×0.8*, 3.277*{span.arrow}×0.8*, 2.621*{span.arrow}×0.8*, 2.097*{span.arrow}×0.8*, …

定义

如果你比较这两个问题，你可能会发现有许多相似之处：哈雷彗星的序列在相邻项之间有相同的，而网球的反弹在相邻项之间有相同的。

具有这些属性的序列有个特殊名称：

一个算术序列在相邻项间有一个常数__{.m-red}差d__。

各项加上或减去同一个数字后，可以得到它的下一项。

一个几何序列在相邻项间有一个常数__{.m-green}比率r__。

各项乘以或除以同一个数字后，可以得到它的下一项。

下面是几个不同的序列。你能确定哪些是算术序列、哪些是几何序列，哪些两个都不是? 能进一步确定它们的_{.b.m-red}d_值或_{.b.m-green}r_值吗？

2, 4, 8, 16, 32, 64, …

是 , 比率为 .

2, 5, 8, 11, 14, 17, …

是 , 差为 .

17, 13, 9, 5, 1, –3, …

是 , 差为 .

2, 4, 7, 11, 16, 22, …

是 .

40, 20, 10, 5, 2.5, 1.25, …

是 , 比率为 .

要定义一个算术序列或几何序列，我们不仅要知道公有的差或比率，还要知道初项值(称为a)。在这里，你可以通过更改a、_d_和_r_的值来生成自己的序列，并将它们的值绘制在图表上。你能找出任何模式吗？

算术序列

a = ${a}, d = ${d}

${arithmetic(a,d,0)}, ${arithmetic(a,d,1)}, ${arithmetic(a,d,2)}, ${arithmetic(a,d,3)}, ${arithmetic(a,d,4)}, ${arithmetic(a,d,5)}, …

几何序列

a = ${b}, r = ${r}

${geometric(b,r,0)}, ${geometric(b,r,1)}, ${geometric(b,r,2)}, ${geometric(b,r,3)}, ${geometric(b,r,4)}, ${geometric(b,r,5)}, …

注意，所有__{.m-red}算术序列__看起来非常相似: 如果差为正，则它们稳定地；而如果差为负，则它们稳定地。

另一方面，几何序列会由于a和r的不同值而展现出完全不一样的曲线行为。

如果 , 则后面项将, 直到无穷。数学家称该序列发散.

如果之间, 后面项将总是 . 我们称该序列收敛.

如果，则后面项将在正数和负数之间交替，而它们的将变大。

关于收敛和发散你将在本课的最后一节学习更多。

递归和显式公式

在上一节中，你学到一个递归公式通过用前面项的函数来告知你每个项的值。以下是算术序列和几何序列的递归公式:

xn=

递归公式有一个问题是找到一个项的值可能会花费很长时间，例如要找到第100项，我们首先必须计算前面的99项。相反，我们可以尝试找到一个显式公式, 它直接告诉我们第n项的值。

对于 算术序列, 我们需要在每一步加 d :

x1= a

x2= a+d

x3= a+d+d

x4=

x5=

在第 n 项, 我们加了个同样的 d, 所以通项公式是:

xn=a+d×n−1.

对于 几何序列, 我们每步乘以_r_:

x1=a

x2=a×r

x3=a×r×r

x4=

x5=

在第n项, 我们乘了个同样的 r, 所以通项公式是

xn=a×rn−1.

以下是到目前为止你所看到的所有定义和公式的摘要：

一个__{.m-red}算术序列__有个首项a，在相邻的项之间有共同的差d。

递归公式: xn=xn−1+d

显式公式: xn=a+d×n−1

一个__{.m-green}几何序列__有个首项a，在相邻的项之间有共同比率r。

递归公式: xn=xn−1×r

显式公式: xn=a×rn−1

现在让我们来看一些能够使用所有这些知识的例子！

让爱传出去

这是电影_让爱传出去_的一个简短片段，12岁的特雷弗在其中解释了他让世界变得更好的想法：

特雷弗的想法的本质是，如果每个人都“让爱传出去”，那么一个人就可以对世界产生巨大的影响：

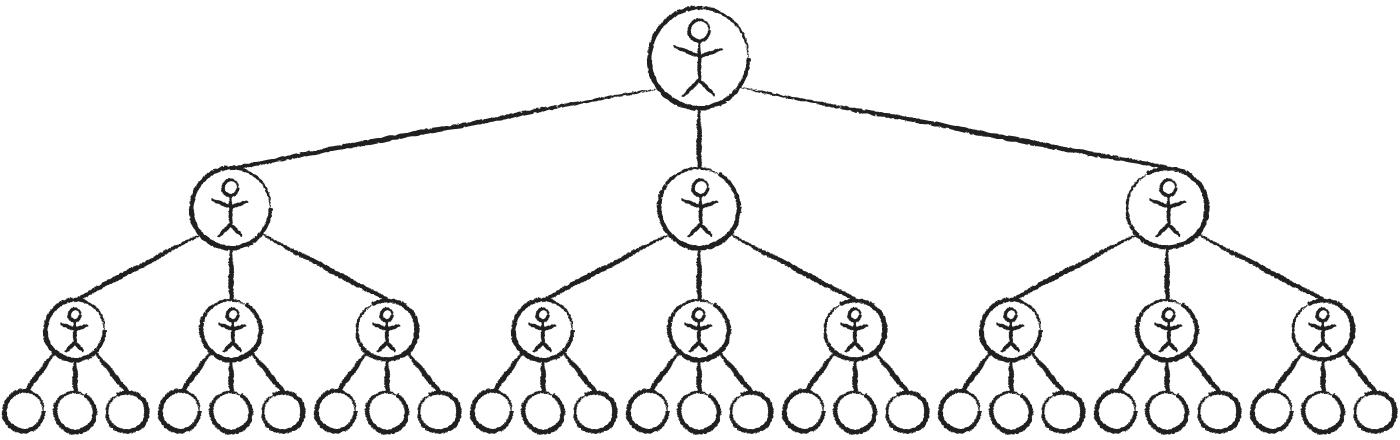
注意每一步的人数是如何形成一个具有比率__的。

1, 3*{span.arrow}×3*, 9*{span.arrow}×3*, ×3, ×3, ×3, …

使用几何序列的显式公式，我们可以计算出在任何步骤中有多少新用户受到影响：

xn =

人数增长得惊人之快。在第10步中，你将达到19683个新的目标，在22步之后，你将到达比现在存活地球的人还多。

这个数字序列有一个特殊的名字：3的幂。如你所见，每一项实际上只是3的不同次幂:

30, 31, 32, 33, 34, 35, …

谁想成为百万富翁？

敬请期待!

棋盘问题