序列和模式斐波那契序列
想象一下,你收到了一对小兔子,一只雄兔和一只雌兔。它们是非常特别的兔子,因为 它们永远不会死,而雌兔每月正好生一对新的兔子(总是另一对雄兔和雌兔)。




















在接下来1个月你会有13对兔子:8对是上月已有的,加上5对新生兔宝宝。你能检测出 这个序列中的模式吗?
某个月内兔子的数量是
再过几个月后,你能计算出兔子的数目吗?
1, 1, 2, 3, 5, 8,
如此12个月后,你将有144对兔子!
这个数字序列称为
当斐波那契于1175年出生时,欧洲的大多数人仍然使用
当他回到意大利后,斐波那契写了一本书,名叫《Liber Abaci》(拉丁语,意为“计算之书”), 在那里他首次向欧洲商人介绍了新的阿拉伯数字。它们立即获得了欢迎 — 直到今天我们 仍在使用它们。
在他书中的一页上,他还研究了兔子的繁殖模式 — 这就是为什么斐波那契数是以他的名 字命名。
来自斐波那契的书 Liber Abaci
当然,斐波那契数并不是兔子在现实生活中的_实际_数量。兔子不是每个月生恰好一个 雄兔和一个雌兔后代,我们也甚至当作兔子不会死。
但事实证明,自然界中还有许多其它地方_确实_体现出斐波那契数,例如植物的螺旋。 你能计算出每个方向有多少个螺旋吗?
这个松果有
这个太阳花有 34 顺时针螺旋同时 有 55 个逆时针螺旋。
在这两种情况下,螺旋的数目都是连续的斐波那契数。其他许多植物也是如此:下次你出去的时候,数一数一朵花的花瓣数,或者一根茎上的叶子数。你经常会发现它们是斐波那契数!
当然,这不仅仅是巧合。自然喜欢斐波那契序列有一个很重要的原因,稍后你将进一步了解。
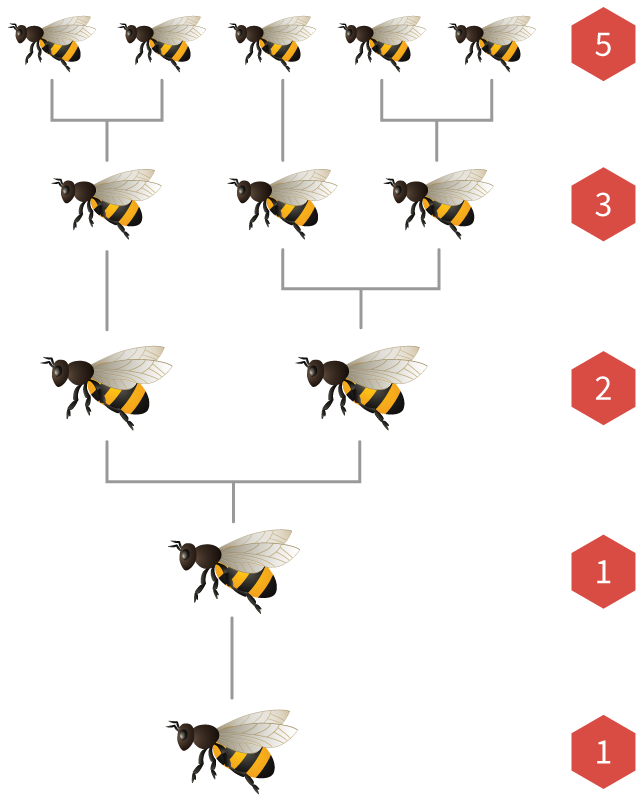
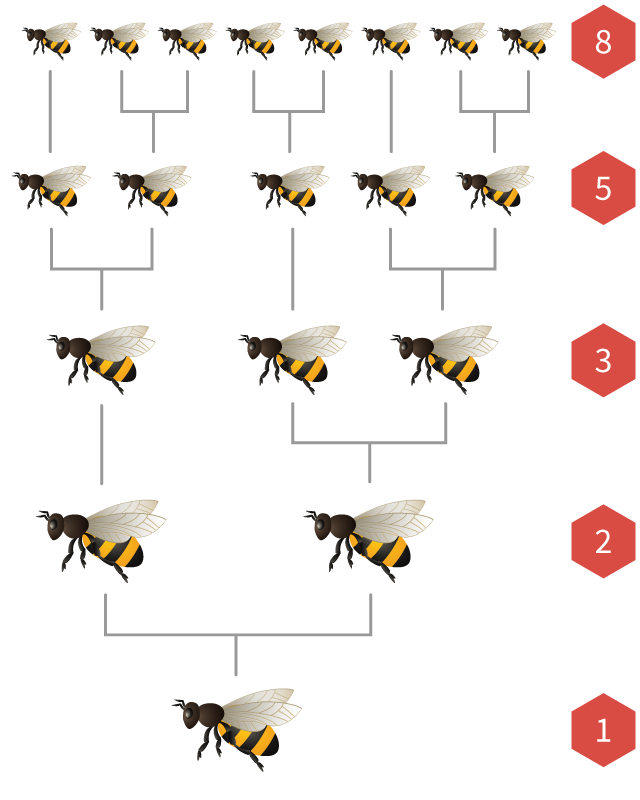
斐波那契数也出现在蜜蜂种群中。
在每一个蜂群中,都有一个_蜂后_产下许多卵。如果一个卵被一只雄性蜜蜂受精,它就会 孵化成一只__雌性__蜜蜂。如果没有受精,它就会孵化成一只__雄性__蜜蜂(被称为雄蜂)。
这意味着雌蜂有
如果我们画出一只蜜蜂的祖先树图,父母、祖父母、 曾祖父母和前几代的数量总是斐波那契数!
偶尔,有些年幼的蜜蜂被喂以 称为“蜂王浆”的特殊食物。在这种情况下,它们会变成蜂后, 然后飞走开始新的蜂巢。
黄金分割率
就像
在每一步,正方形形成一个更大的矩形。它的宽度和高度总是两个连续的斐波那契数。 矩形的__纵横比__是其宽度和高度的比:
注意,随着我们添加越来越多的正方形,纵横比似乎越来越接近于1.6左右的特定数字。 这个数字被称为
许多人认为黄金分割比在美学上特别令人愉悦。这就是为什么艺术家和建筑师经常使用它, 就像这两个例子:

据说希腊雕塑家菲迪亚斯在雅典设计_帕台农神庙_时使用了黄金比例。他名 字的第一个字母

西班牙艺术家萨尔瓦多·达利的 最后的晚餐圣礼 是许多应用了黄金比例 的画作之一。在背景中,你还可以看到一个大的
我们可以用斐波那契数的两个连续项
然而,事实证明,
斐波那契螺旋
黄金分割率解释了为什么斐波那契数出现在自然界中,就像你在本节开头看到的向日葵 和松果。
这两种植物都从中心(植物上叫做_分生组织_的部分)向外生长。当新的种子、叶子或花瓣 被添加时,它们将现有的种子、叶子或花瓣进一步推向外部。
移动右边的滑块来可视化展示植物的生长方式。请注意,每个叶是如何以不同于前一个 叶的旋转方式添加的。两个连续叶之间的角度总是相同的。
对于花来说,选择一个合适的角度是很重要的:叶子或种子必须大致等距分布,这样它们 才能获得最大的阳光和营养。在下面的图表中,你可以探索向日葵种子之间不同角度的外观:
不幸的是,“臂”不好,因为它们意味着种子分布不均匀:臂之间的所有空间都被浪费了。 但是如果
你可能记得从上面,续斐波那契数的比率越来越接近黄金比率——这就是为什么,如果 你计算一个植物的螺旋数,你会经常发现斐波那契数。
重要的是要记住,自然界并不知道斐波那契数。自然也无法解出方程来计算黄金分割 比——但在数百万年的过程中,植物有足够的时间尝试不同的角度并发现最佳角度。
植物和动物总是希望以最有效的方式生长,这就是为什么自然界充满规则的数学模式。
菲波那科斯
到目前为止,我们只使用了斐波那契数的递推方程。实际上,也有一个显式的方程 式——只是更难找到它:
我们也可以尝试为斐波那契数选择不同的起始点。例如,如果我们从2,1开始, …,而不是 1,1开始,…,我们得到一个序列,它叫做__卢卡斯序列__。
结果表明,无论你选择哪两个起始数字,结果序列都共有许多属性。例如,连续项的 比将_总是_
还有许多其他的谜题、模式和应用与斐波那契数相关。以下是几个例子,你可以自己尝试:
问题求解
1. 斐波那契整除性
(a) 哪些斐波那契数是偶数?,它们在序列中的位置是否有一个模式?你能解释为什么吗?
(b) 哪些斐波那契数可被3整除(或可被4整除)?你注意到什么了?
2. 斐波那契和
如果你把三个连续的斐波那契数加起来会怎么样?你能解释为什么吗?
3. 斐波那契楼梯
当上楼梯时,我既可以一步上一阶楼梯,也可以一步上两阶楼梯。这意味着上楼梯的方 式有很多不同的可能性。例如,如果有5阶楼梯,我们有8种不同的选择:
对6、7或8阶楼梯有多少种选择?你能发现一个模式吗?这和斐波那契数有什么关系?
© FoxTrot, by Bill Amend