Untitled Course对称组和墙纸
有些形状具有多个对称性-让我们以一个简单的例子来看一下








上面已经显示了一个正方形具有
它还具有
最后,我们可以将“什么都不做”考虑为另一种特殊的对称性-因为结果(显然)与以前相同。有时称为__身份__ 。
总共,我们发现了
现在,我们实际上可以开始对这些对称性进行一些算术运算。例如,我们可以_添加_两个对称以获得新的对称:






只要添加一个正方形的两个对称,就可以得到一个新的对称。这是一个“对称计算器”,您可以自己尝试:
花一些时间玩对称计算器,然后尝试找到任何模式。你能完成这些观察吗?
*增加两个旋转将始终产生
您可能已经意识到添加__{.orange}对称__实际上与添加非常相似__{.green}整数__ :
- Adding two symmetries/integers always gives another symmetry/integer:
+ = 12 + 7 = 19 - Adding symmetries/integers is
associative :+ + = + + 4 + 2 + 5 = 4 + 2 + 5 - Every symmetry/integer has an inverse, another symmetry/integer which, when added, gives the identity:
+ = 4 + –4 = 0
在数学中,具有这些属性的任何集合都称为
在此示例中,我们从正方形的八个对称开始。实际上,每个几何形状都有自己的__对称组__ 。它们都有不同的元素,但是它们始终满足上述三个规则。
组在数学中无处不在。元素可以是数字或对称性,也可以是多项式,置换,矩阵,函数…… _任何_符合这三个规则的东西。 _小组理论_的关键思想是,我们对单个元素不感兴趣,而对_它们之间如何相互作用_不感兴趣。
例如,不同分子的对称基团可以帮助科学家预测和解释相应材料的特性。
小组还可以用来分析棋盘游戏的制胜策略,药物中的病毒行为,音乐中的不同谐调以及许多其他概念……
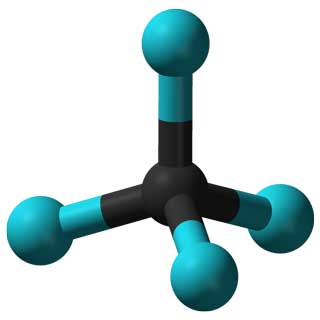
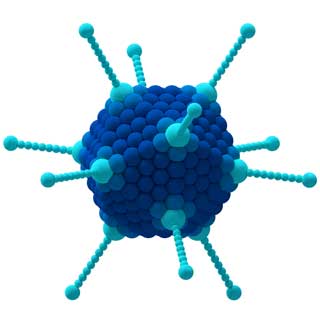
CCl 4分子(左)和腺病毒(右)的特性由它们的对称性决定。
墙纸组
在前面的部分中,我们看到了与两种不同的变换相对应的两种不同的对称性:旋转和反射。但是,第三种刚性转换也具有对称性:


六角形蜂窝


陶瓷墙地砖
除了反射,旋转和平移对称性之外,还有第四种类型:


图案可以具有不止一种类型的对称性。就像正方形一样,我们可以找到模式的
这些小组并没有告诉您有关图案的_外观_ (例如颜色和形状)的更多信息,而只是告诉您如何_重复_图案。多个不同的模式可以具有相同的对称组-只要以相同的方式排列和重复该模式即可。


这两种模式具有相同的对称性,即使它们看起来非常不同。但是对称性与颜色或表面形状无关。


这两种模式也具有相同的对称性-即使它们看起来更类似于左侧的对应模式,而不是彼此相似。
事实证明,尽管存在无限多种可能的模式,但它们都只有17个不同的对称组之一。这些称为__墙纸组__ 。每个墙纸组均由平移,旋转,反射和滑动反射的组合定义。您可以在这些示例中看到

Group 1 – P1
Only translations div img(src="/content/transformations/images/wallpapers/p2.svg" width=360, height=240) p.caption Group 2 – P2 Rotations of order 2, translations div img(src="/content/transformations/images/wallpapers/p3.svg" width=360, height=240) p.caption Group 3 – P3 Rotations of order 3 (120°), translations div img(src="/content/transformations/images/wallpapers/p4.svg" width=360, height=240) p.caption Group 4 – P4 Four rotations of order 2 (180°), translations div img(src="/content/transformations/images/wallpapers/p6.svg" width=360, height=240) p.caption Group 5 – P6 Rotations of order 2, 3 and 6 (60°), translations div img(src="/content/transformations/images/wallpapers/pm.svg" width=360, height=240) p.caption Group 6 – PM Parallel axes of reflection, translations div img(src="/content/transformations/images/wallpapers/pmm.svg" width=360, height=240) p.caption Group 7 – PMM Perpendicular reflections, rotations of order 2, translations div img(src="/content/transformations/images/wallpapers/p4m.svg" width=360, height=240) p.caption Group 8 – P4M Rotations (ord 2 + 4), reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/p6m.svg" width=360, height=240) p.caption Group 9 – P6M Rotations (ord 2 + 6), reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/p3m1.svg" width=360, height=240) p.caption Group 10 – P3M1 Rotations of order 3, reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/p31m.svg" width=360, height=240) p.caption Group 11 – P31M Rotations of order 3, reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/p4g.svg" width=360, height=240) p.caption Group 12 – P4G Rotations (ord 2 + 4), reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/cmm.svg" width=360, height=240) p.caption Group 13 – CMM Perpendicular reflections, rotations of order 2, translations div img(src="/content/transformations/images/wallpapers/pmg.svg" width=360, height=240) p.caption Group 14 – PMG Reflections, glide reflections, rotations of order 2, translations div img(src="/content/transformations/images/wallpapers/pg.svg" width=360, height=240) p.caption Group 15 – PG Parallel glide reflections, translations div img(src="/content/transformations/images/wallpapers/cm.svg" width=360, height=240) p.caption Group 16 – CM Reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/pgg.svg" width=360, height=240) p.caption Group 17 – PGG Perpendicular glide reflections, rotations of order 2, translations
不幸的是,没有简单的理由说明为什么有_17_个这样的小组,要证明这一点需要更高级的数学。相反,您可以尝试为17个壁纸组的每一个绘制自己的重复图案:
Examples of other students’ drawings



墙纸组都是关于平面二维图案的。我们可以对三维图案进行类似的处理:这些称为晶体学群,其中有219个!
除了平移,反射,旋转和滑行反射之外,这些组还包括__滑行平面__和__螺旋轴之__类的对称性(拧开瓶子时请考虑一下运动)。
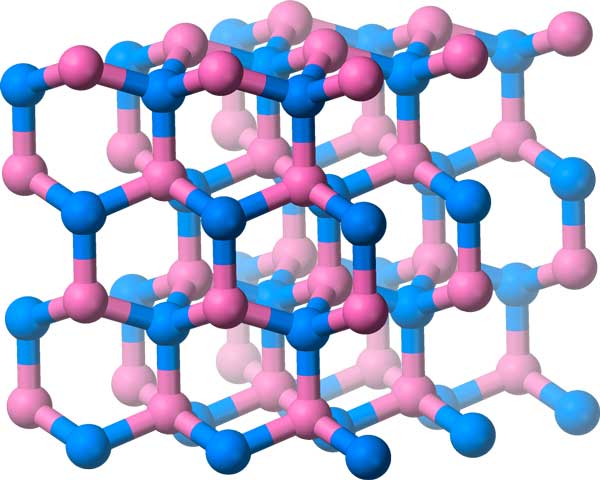
氮化硼的分子排列在具有三维对称基团的该晶格中。