Untitled Course镶嵌

多边形在自然界中无处不在。如果要平铺较大的区域，它们特别有用，因为可以将多边形组合在一起而没有任何间隙或重叠。像这样的模式称为镶嵌 。

从古罗马到现在，人类已经在艺术，建筑和技术中复制了许多自然形态。这里有一些例子：

在这里，你可以使用正多边形创建自己的镶嵌。只需将新形状从侧边栏拖动到画布上即可。哪些形状的镶嵌效果好？有没有完全不能镶嵌的形状？尝试创建有趣的模式！

别的学生创建的镶嵌图案例子

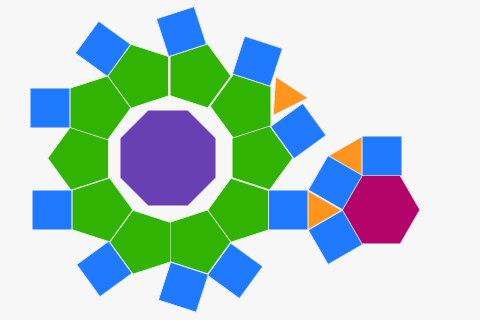
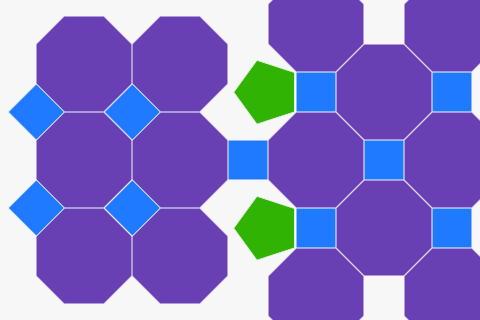
来自正多边形的镶嵌

你可能已经注意到一些正多边形(例如正方形正五边形)非常容易镶嵌，而另外一些（例如五边形三角形六角形)似乎根本没有法镶嵌。

这与其内角的大小有关，这是我们之前学过的计算。在镶嵌中的每个顶点处 ，多个不同多边形的内角相交。我们需要所有这些角度加起来达到°，否则将存在间隙或重叠。

你可以类似地检查其它，就像五边形那样，具有7个或更多边的常规多边形不可镶嵌。这意味着能够镶嵌的正多边形只有是等边三角形，正方形和正六边形！

当然，你可以将不同种类的正多边形组合在一起进行镶嵌，前提是它们的内角之和正好为360°：

正方形和等边三角形
90° + 90° + 60° + 60° + 60° = 360°

正方形和等边三角形
90° + 90° + 60° + 60° + 60° = 360°

正六边形和等边三角形
120° + 120° + 60° + 60° = 360°

正六边形和等边三角形
120° + 60° + 60° + 60° + 60° = 360°

正六边形，正方形和等边三角形
120° + 90° + 90° + 60° = 360°

正八边形和正方形
135° + 135° + 90° = 360°

正十二等边和等边三角形
150° + 150° + 60° = 360°

正十二边形，正六边形和正方形
150° + 120° + 90° = 360°

非正多边形的镶嵌

我们也可以尝试使用非正多边形制作镶嵌，只要小心旋转和排列它们即可。

五边形点棘手。我们已经看到 正 五边形不能镶嵌能镶嵌 ，非正五边形呢？

这是五边形镶嵌的三个不同示例。它们不是 正 五边形 ，但它们是完全有效的5边形。

到目前为止，数学家仅发现了15种带有（凸）五边形的镶嵌图案-最近的是在2015年发现的。

两年之后的2017年, 米夏埃尔·拉奥 发表了一份证明：除了已经找到的15个，没有其它的可能性了。你能用它们来做镶嵌吗？

艺术镶嵌

许多艺术家，建筑师和设计师在他们的作品中使用镶嵌图案，其中最著名的是荷兰艺术家M·C·埃舍尔。他的作品包含奇怪的，变异的生物，图案和风景：

这些艺术品通常看起来既有趣又轻松，但其基本的数学原理与以前相同：角度，旋转，平移和多边形。如果数学不正确，则镶嵌将无法生效！

蜕变 II” M·C·埃舍尔 (1940)

彭罗斯瓷砖

到目前为止，我们看到的所有镶嵌图都有一个共同点：它们是 周期性的 。这意味着它们由规则模式组成，该模式会一次又一次地重复。它们可以在所有方向上永远持续下去，并且到处看起来都一样。

在1970年代，英国数学家和物理学家罗杰·彭罗斯发现了 非周期性的 镶嵌结构-它们仍然在各个方向上无限地延续，但看上去 决不会 完全相同。这些称为 彭罗斯瓷砖 ，并且你只需要几种不同的多边形即可创建一个：

彭罗斯（Penrose）纯粹是出于娱乐目的而探索镶嵌，但事实证明，某些真实材料（如铝）的内部结构遵循类似的模式。该图案甚至被用在厕纸上，因为制造商注意到可以将非周期性的图案卷起而没有凸起。