Untitled Course柏拉图多面体

在本课程开始时，我们将正多边形定义为特别“对称”的多边形，其中所有边和角度都相同。我们可以为多面体做类似的事情。

在 正多面体 中，所有面都是相同种类的正多边形，并且在每个顶点处都遇到相同数量的面。具有这两种特性的多面体被称为柏拉图多面体 ，以希腊哲学家柏拉图命名。

那么柏拉图多面体是什么样子？其中有多少种？要制作三维形状，我们需要在每个顶点至少有个面相交。让我们从最小的规则多边形开始：等边三角形：

每个顶点上七个或更多的三角形也不会产生新的多面体：顶点周围没有足够的空间来容纳那么多三角形。

这意味着我们已经找到了由三角形组成的个柏拉图固体。让我们继续下一个常规多边形：正方形。

接下来，让我们尝试正五边形：

如果在每个顶点有个五边形相遇，我们得到 十二面体 。它有个面。 （“Dodeca”在希腊语中意为“十二”。）

下一个要尝试的规则多边形是六边形：

如果每个顶点都有三个六边形，我们会立即得到镶嵌多面体六面体 。 由于没有超过三个六边形的空间，因此似乎没有由六边形组成的柏拉图多面体。

具有六个以上边的所有正多边形也会发生同样的情况。它们不会镶嵌，我们当然也不会得到任何三维多边形。

这意味着只有种柏拉图固体！让我们一起看看所有这些：

注意在立方体和八面体间变化时面和顶点的数量是如何交换维持不变的，以及十二和二十面体的边是如何保持相同变成不同的。这些成对的柏拉图多面体称为双重多面体 。

我们可以通过用顶点“替换”每个面，以及用面“替换”每个顶点来将一个多面体变成其对偶的。这些动画展示了是怎么转化的：

正四面体本身是双重的。由于它具有相同数量的面和顶点，因此交换它们不会改变任何东西。

柏拉图认为，宇宙中的所有物质都由四个元素组成：空气，土，水和火。他认为每个元素都对应一种柏拉图多面体，而第五种元素则代表整个宇宙。今天，我们知道有100多种不同的元素由球形原子组成，而不是多面体。

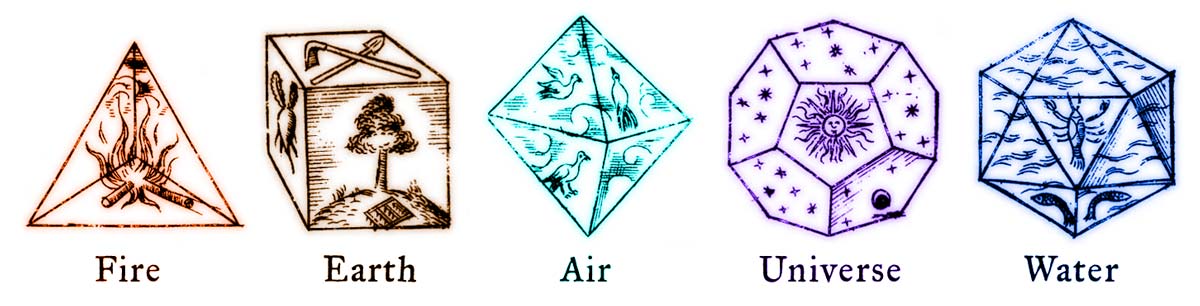
图片来自约翰内斯·开普勒的《和谐世界》(1619)

阿基米德多面体

柏拉图多面体是特别重要的多面体，但还有无数其他的。

例如， 阿基米德多面体仍然必须由正多边形组成 ，但是你可以使用多种不同的类型。它们以另一位希腊数学家锡拉丘兹的阿基米德命名，其中13种：

应用领域

柏拉图认为所有元素都由柏拉图多面体组成是错误的。但是普通的多面体具有许多特殊性质，使它们出现在自然界的其它地方–我们可以在科学和工程学中复制这些性质。