三角形与三角学三角形的性质
让我们从最简单的开始:一个三角形是一个封闭形状,由三条边(这些边是
我们可以根据内角大小对三角形进行分类:
直角三角形 有一个
钝角三角形 有一个
锐角三角形 有
为了方便起见,我们总是用统一的方式来标记三角形,顶点用大写字母 A, B 和 C 来表示,边用小写字母 a, b 和 c 来表示,角用希腊字母
位于 顶点 A 对面一侧的边 标记为 a,顶点两侧线所夹的角 标记为
中线
这里你可以看到一个三角形以及它三条边的
三角形的
看起来中线总是
中线总是将其它两条中线按 2:1 比率 分开,对于每条中线来说,从顶点到形心的距离总是
形心也是三角形的「平衡点」。在硬纸板上画一个三角形,把它剪下来,找出三条中线,只要画得准确,你就可以用铅笔顶起三角形纸板,或者把它悬挂在一根绳子上,这根绳子连着它的质心,三角形纸板都可以保持平衡:
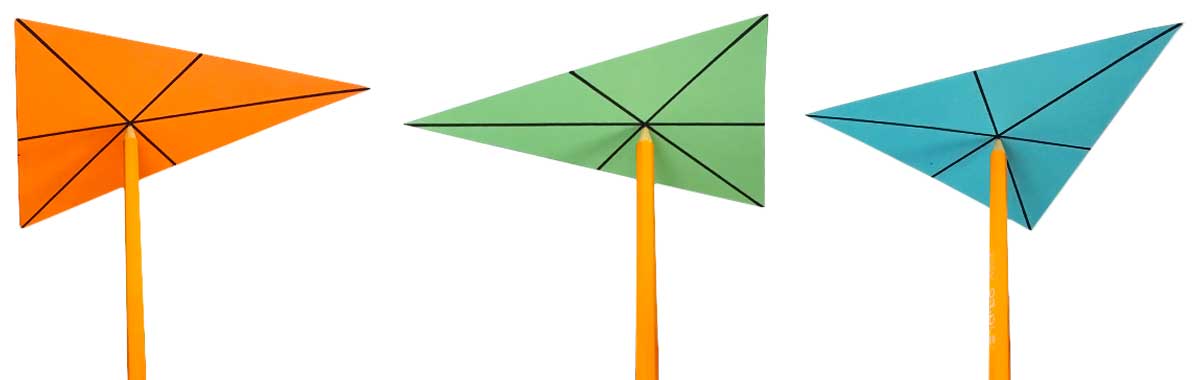
这是因为三角形的重量平均分布在了形心的周围,在物理学中,这个点也叫做 重心。
垂直平分线与外接圆
回想一下,一条线的
画出旁边三角形三条边的垂直平分线。 要绘制三角形一条边的垂直平分线,只需要单点一个端点并拖动到另一个端点。
和之前一样,三条垂直平分线相交于一点,这个点也有一个特殊的性质。
垂直平分线上的任意一点到它所平分直线的两个端点的距离相等。例如,蓝色平分线上的任意一点到点 A 和 C 的距离相等,红色平分线上的任意一点到点
交点位于三条垂直平分线上,因此它到三角形的三个
这意味着我们可以以交点为圆心,过三个顶点作一个圆,这个圆叫做三角形的
事实上,给定任意三个点,你都可以利用外心去找到一个过这三个点的圆(除非这三个点
角平分线与内接圆
现在你可能已经掌握了窍门: 我们对三角形的每条边/每个角进行一种特定的划分,然后我们找出它们相交位置的特殊之处。
回想一下,
三条平分线又再次相交于同一点,你可能也预料到会这样,但没有明显的理由表明为什么会这样 —— 三角形只是一种非常特殊的形状!
位于角平分线上的点与构成角的两条直线之间的距离相等。例如,蓝色角平分线上的任意点到边 a 和边 b 的距离相等,红色平分线 上的任意点到
交点位于三条平分线上,因此它到三角形的三条
这意味着我们可以以交点为圆心画一个圆,这个圆位于三角形的内部,刚好碰到它的三条边,这个圆叫做三角形的 内切圆,圆心叫做 内心。
面积与高线
求一个
矩形的宽与三角形的 底边 相等 (称为 底),矩形的高是从三角形底到所对顶点的垂直距离 。
高把三角形分为了两部分,需要注意的是矩形中的两个空白间隙恰好与三角形的两个部分一样大,这意味着这个长方形的面积正好是三角形的
矩形的面积很容易知道,所以三角形的面积是:
To calculate the area of a triangle, you can pick any of the three sides as base, and then find the corresponding height, which is the line that is
In triangles, these heights are often called
Like the
In
In
In