三角形与三角学毕达哥拉斯定理

现在我们来到几何学中一个非常重要的内容 -- 理解数学中最著名的定理之一：毕达哥拉斯定理，该定理是以古希腊数学家毕达哥拉斯命名的。

毕达哥拉斯定理 在任意直角三角形中，斜边 (与直角相对的一边)长度的平方等于另外两边的平方和，换句话说，

a2 + b2 = c2

反之亦然：如果三角形的三条边满足 a2+b2=c2，它一定是三角形

直角无处不在，这也是为什么毕达哥拉斯定理如此有用的原因。

在这里你可以看到一个 6米长的梯子斜靠在墙边，梯子的底离墙有 1米远，问墙底到梯子顶部有多远？

注意，梯子、墙壁和地面组成了一个直角三角形，运用毕达哥拉斯定理，可以得到

h2+12	=62
⇒h2	=
⇒h	=35=5.92米

任意情况下，只要你有一个直角三角形，并且知道它的两条边，毕达哥拉斯定理可以帮你得到第三条边。

证明毕达哥拉斯定理

毕达哥拉斯定理为古巴比伦人、美索不达米亚人、印度人和中国人所熟知，但毕达哥拉斯可能是第一个从数学上正式证明它的人。

事实上有许多不同的方法来证明毕达哥拉斯定理，这里我们来看其中三个，每一个都使用了不同的策略来完成证明：

重新组合

看看右图，正方形的边长为 a + b ，它里面包含四个直角三角形，以及一个面积为的小正方形。

现在让我们对正方形中的三角形进行重新组合，结果仍然包含这四个直角三角形，以及两个面积大小为的正方形。

比较重组前和重组后红色区域的面积大小，我们可以看到：

a2+b2=c2.

这是毕达哥拉斯的原始证明。

c²

a²

b²

代数

这里我们有一幅一样的图，但这次我们将使用代数而不是 重新排列 来证明毕达哥拉斯定理。

大正方形边长为 a+b ，面积为。

大正方形由四个三角形以一个小正方形组成，每个三角形的面积为，小正方形的面积为。

如果把这些信息结合起来，可以得到：

a+b2	=4×12ab+c2
a2+2ab+b2	=2ab+c2
a2+b2	=c2

我们再一次证明了毕达哥拉斯定理。

相似三角形

这里你可以看到一个直角三角形，画出它的高，高将其分成两个小三角形，也将三角形的斜边 c 分成两小段，分别命名为 x 和 y。继续

让我们把两个小三角形分开，这样可以更清楚地看到它们之间的关系... 继续

两个小三角形与原来的三角形有一个共用角，它们都有一个直角，根据 AA 条件判定，这里的三个三角形一定。

现在我们可以使用我们已经知道的相似三角形公式：

xa=ac

x=a2c

yb=bc

y=b2c

继续

而 c = x + y，因此

c=a2c+b2c

c2=a2+b2

我们再一次证明了毕达哥拉斯定理

关于毕达哥拉斯的生平很多是未知的，也没有什么原始的作品留存下来，他创立了一个宗教学派 -- 毕达哥拉斯学派 ，对数字痴迷到几近崇拜，他们认为所有的数字都有其自身的特性，并遵循着各种奇怪的习俗。

毕达哥拉斯学派有许多数学发现，包括发现第一个无理数：2。无理数不能用简单的分数来表示 -- 毕达哥拉斯学派发现了这个令人不安的概念，并试图掩盖它（但没有成功）！

“Pythagoreans celebrate sunrise” by Fyodor Bronnikov

计算距离

毕达哥拉斯定理一个重要的应用就是计算距离。

在右侧你可以看到坐标系中有两个点，我们可以用尺子测量它们的距离，但这并不是特别准确，但我们可以使用毕达哥拉斯定理。继续

我们可以很容易计算出沿 x 轴的水平距离和沿 y 轴的垂直距离，如果画出这两条线，我们就得到了一个直角三角形。

利用毕达哥拉斯定理，

d2	=${b.x-a.x}2+${b.y-a.y}2
d2	=${(b.x-a.x)(b.x-a.x) + (b.y-a.y)(b.y-a.y)}
d	=${(b.x-a.x)2+(a.y-b.y)2}=${round(distance(a,b),4)}

这个方法适用于计算任意两点之间的距离：

距离公式 如果给定两个坐标点 (x1,y1) 和 (x2,y2)，它们之间的距离是

d2=x2−x12+y2−y12

d=x2−x12+y2−y12

毕达哥拉斯三元组

当你移动三角形的顶点时，可能已经注意到，大多数情况下，斜边 d 的长度为。然而，有几个直角三角形的例子，它们三条边的长度恰好是整数。

一个著名的例子是 3-4-5 三角形，由于 32+42=52，因此边长为3，4，5的三角形一定是直角三角形。

古埃及人不知道毕达哥拉斯定理，但他们知道 3-4-5 三角形。在建造金字塔的时候，他们使用的就是长度为3，4，5的打结绳来测量完美直角。

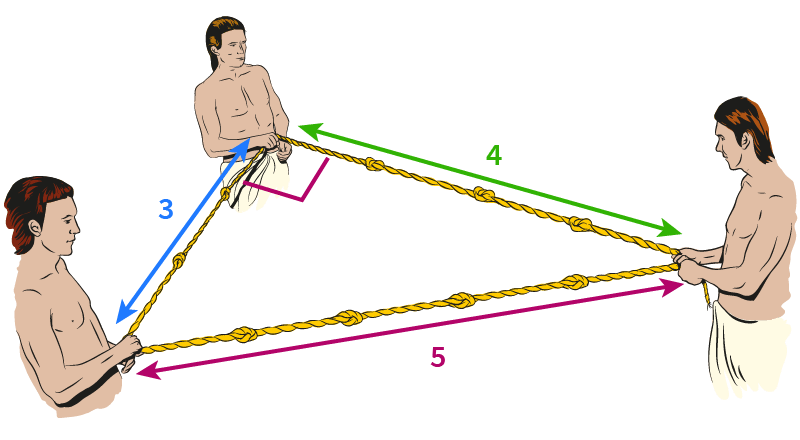
像这样的三个整数就叫做毕达哥拉斯三元数（中文里又叫勾股数），(3, 4, 5)就是一组毕达哥拉斯三元数，如果把每个数字乘以2，我们可以得到另一个毕达哥拉斯三元数：(6, 8, )。

我们可以把这些三元数看作坐标系中的网格点，对于一个有效的毕达哥拉斯三元组来说，从原点到网格点的距离必须是整数，在下面的坐标系中，你能找到其它的毕达哥拉斯三元组吗？

${a.x}

${a.y}

${round(a.length,2)}

你注意到这些点的分布有什么规律吗？

更改语言

登录到Mathigon

分享

重置进度

词汇表